De él se ha dicho

"Pienso que todo esto debe ser más que una coincidencia y creo que está tocando algo profundo."
David Finkelstein

"es uno de los modelos de unificación más convincentes que he visto en muchos, muchos años."
Lee Smolin


"Cuando comencé a leer el artículo era escéptico. Cuando terminé, me pregunté porqué no se me había ocurrido la idea antes."
Carlo Rovelli


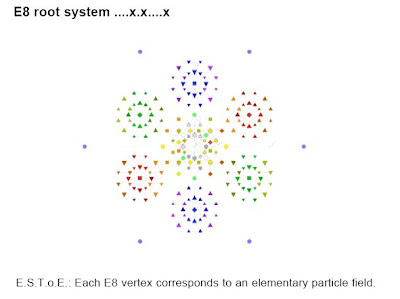
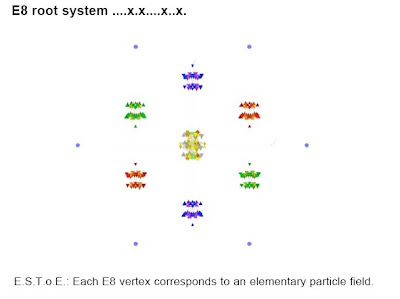
" Lisi's inspiration lies in the most elegant and intricate shape known to mathematics, called E8 - a complex, eight-dimensional mathematical pattern with 248 points first found in 1887, but only fully understood by mathematicians this year after workings, that, if written out in tiny print, would cover an area the size of Manhattan."
Roger Highfield, Science Editor

E8 - Una teoría excepcionalmente simple

El físico norteamericano Garrett Lisi está revolucionando el mundo de la física teórica con un modelo matemático que, supuestamente, podría reflejar todas las partículas que componen la materia y todas las interacciones entre ellas, incluidas la de la gravedad, que hasta la fecha había sido la piedra en el zapato de la llamada teoría del todo.

Hasta el momento, el modelo geométrico propuesto por Lisi parece ser verdaderamente el espejo de la forma de funcionar de la naturaleza, según las observaciones realizadas. Habrá que esperar sin embargo a que se ponga en marcha el Gran Colisionador de Hadrones de Ginebra para comprobar más a fondo su teoría. De funcionar, según Lisi, se demostraría que el universo es una estructura geométrica de una belleza excepcional.

Periodic table. G2 in SO(7), F4 Root System

E8 root system